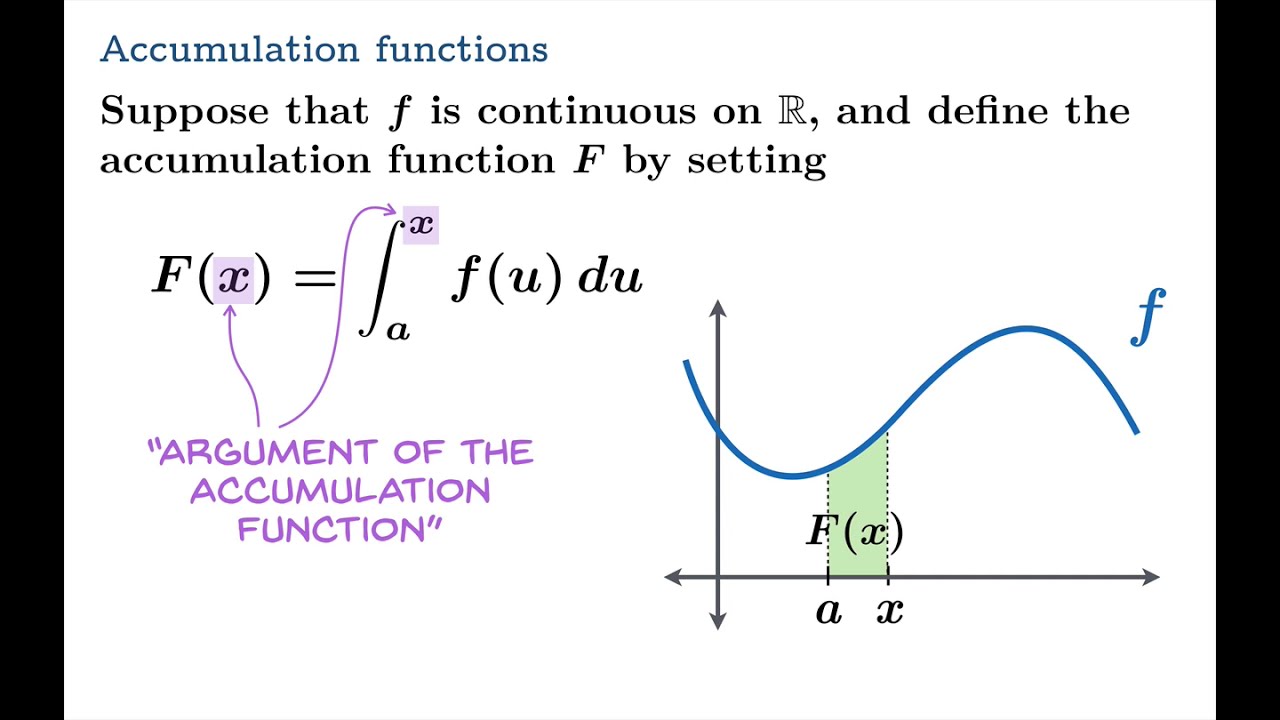
fokicoupon.blogg.se - Fundamental theorem of calculus part 2

#FUNDAMENTAL THEOREM OF CALCULUS PART 2 MANUAL#

Note that even though F(x) is defined in terms of the integral of another function, which may seem confusing since we expect a definite integral to be a number, the result of the integral for any given x value is indeed a number. It is new, very important because it is always on the AP exam, and I will refer to the process as 'using the FTC'. In other words, the area under the curve is represented by: AP Calculus 1 The Fundamental Theorem of Calculus Part 2 This part of the Fundamental Theorem of Calculus tells us what happens when you take the derivative of an integral that has a variable as an upper limit of integration. In the figure, F(x) is a function that represents the area under the curve between a and some point x within the interval. 207 (2nd edition) this section of Simmons is another presentation. Given a function f(t) that is continuous over an interval, recall that an integral represents the area under the curve. The Fundamental Theorem of Calculus really consists of two closely related theorems. It also gives us an efficient way to evaluate definite integrals. The fundamental theorem of calculus (FTC) establishes the connection between derivatives and integrals, two of the main concepts in calculus. The observations made in the preceding two paragraphs demonstrate that differentiating and integrating (where we integrate from a constant up to a variable) are almost inverse processes.Home / calculus / integral / fundamental theorem of calculus Fundamental theorem of calculus At right, the antiderivative function \(F(x) = \frac\) At left, the graph of \(f(x) = x^2\) on the interval \(\) and the area it bounds.

Population Growth and the Logistic Equationįigure 5.2.1. The second part of the FTC tells us the derivative of an area function.

Qualitative behavior of solutions to DEs.

An Introduction to Differential Equations.

Explain the relationship between differentiation and integration. The fundamental theorem of calculus part 2 states that it holds a continuous function. These two concepts apparently seem to have no relation between them, one arises from an area problem and the other from a tangent problem.

Physics Applications: Work, Force, and Pressure Use the Fundamental Theorem of Calculus, Part 2, to evaluate definite integrals. The Fundamental Theorem of Calculus states the relationship between differentiation and integration of a function.

(Fundamental Theorem of Calculus Part 2) If f(x) is.

Using Definite Integrals to Find Volume We can however use FTC Part 1 to determine a way to calculate definite integrals exactly.

Using Definite Integrals to Find Area and Length.

Other Options for Finding Algebraic Antiderivatives.

The Second Fundamental Theorem of Calculus.

It just says that the rate of change of the area. 1The Indefinite Integral (Antiderivative) finds a Family of Functions whose derivative is given. This means that, very excitingly, now to calculate the area under the curve of a continuous. The fundamental theorem of calculus establishes the relationship between the derivative and the integral. Text of 6034 Fundamental Theorem of Calculus (Part 2).

Constructing Accurate Graphs of Antiderivatives The Fundamental Theory of Calculus part 2 (part i).

Determining distance traveled from velocity.

Using derivatives to describe families of functions.

In the upcoming lessons, we’ll work through a few famous calculus rules and. Fundamental Theorem Of Calculus: The original function lets us skip adding up a gajillion small pieces.

#FUNDAMENTAL THEOREM OF CALCULUS PART 2 MANUAL#

Part 1 said that if we have the original function, we can skip the manual computation of the steps.

Using derivatives to identify extreme values 11.2 Part 2: Finding The Indefinite Integral.Derivatives of Functions Given Implicitly.Derivatives of other trigonometric functions.The Meaning of the Fundamental Theorem of Calculus. Limits, Continuity, and Differentiability Using Part 2 of the Fundamental Theorem of Calculus to find the derivative of an integral closed Ask Question Asked 5 years, 1 month ago. To compute definite integrals using FTC, compute the antiderivative of the function, substitute the upper bound, and subtract substituting the lower bound.Interpreting, estimating, and using the derivative.The derivative of a function at a point.